Quinto Artigo da Série (Ensino de Geometria)
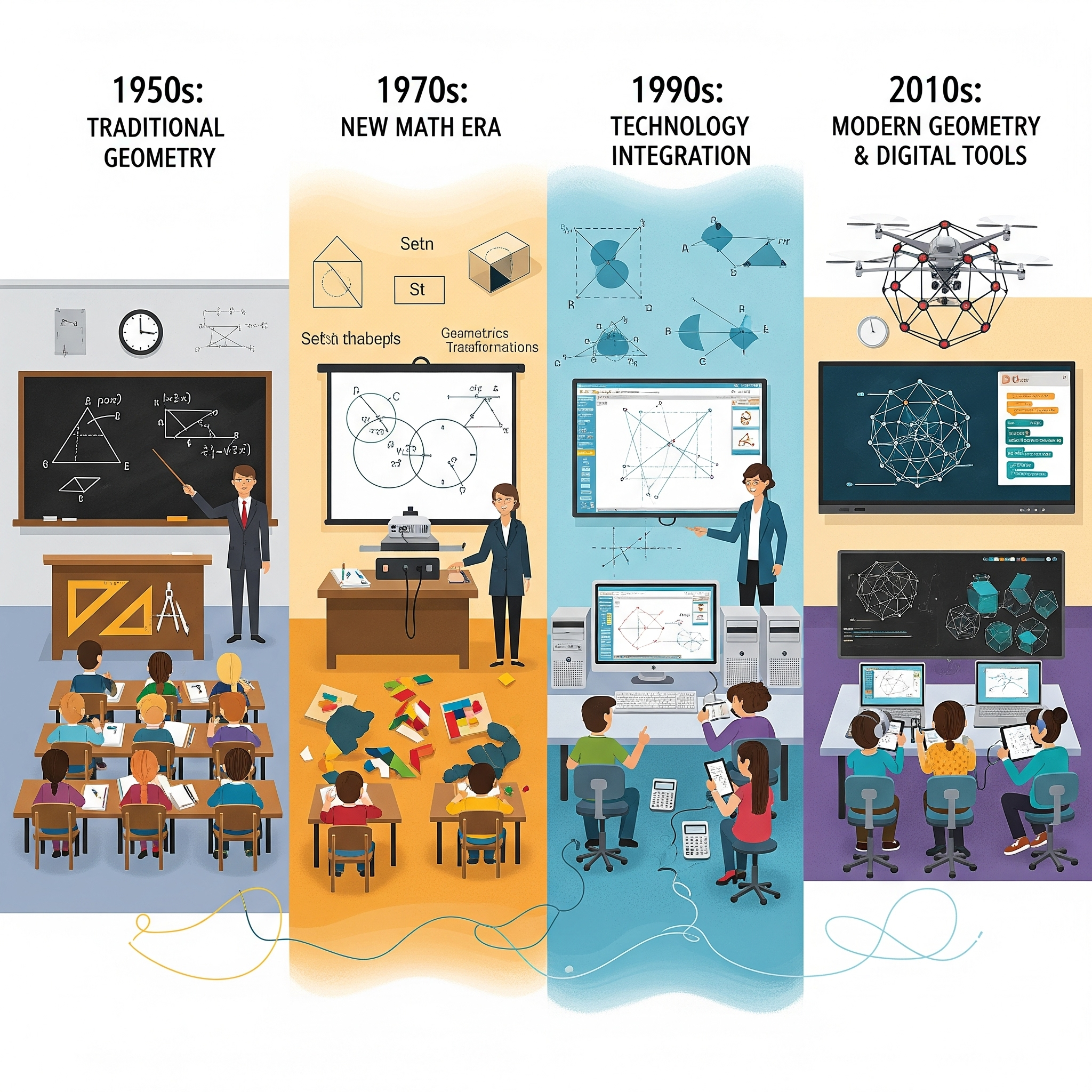
Geometria na BNCC e nos PCNs: O Que Mudou nas últimas décadas?.
O ensino da geometria passou por transformações significativas nas últimas décadas, especialmente com a transição dos Parâmetros Curriculares Nacionais (PCN) para a Base Nacional Comum Curricular (BNCC). Neste post, vamos analisar as principais mudanças e continuidades entre esses dois documentos, destacando como elas impactam o ensino da geometria no ensino médio e nos anos finais do ensino fundamental
RESUMO:
Segundo os autores, as principais diferenças entre os PCNs e a BNCC no ensino de geometria incluem:
Organização dos conteúdos:
PCN: estrutura por ciclos (3º e 4º ciclos).
BNCC: estrutura por ano letivo (6º ao 9º ano e ensino médio).
Enfoque temático:
PCN: eixo chamado Espaço e Forma, com foco na geometria clássica.
BNCC: introduz a geometria das transformações e o uso de tecnologias digitais.
Conteúdos novos na BNCC:
Plano cartesiano desde o 5º ano.
Simetria, semelhança e transformações geométricas.
Algoritmos e fluxogramas para resolução de problemas geométricos.
Integração com outras áreas:
A BNCC enfatiza a interdisciplinaridade e a aplicação da geometria em contextos reais, como engenharia, arte e arquitetura.
NOSSA REFLEXÃO
A BNCC representa um avanço ao tornar o ensino da geometria mais conectado com o cotidiano dos alunos e com as demandas contemporâneas. Ao incluir temas como simetria, transformações e visualização espacial desde os anos iniciais, ela promove uma formação mais sólida e progressiva. No entanto, é essencial que os professores estejam preparados para aplicar essas diretrizes com criatividade e sensibilidade pedagógica.
APLICAÇÃO PRÁTICA
Sugestões para alinhar a prática docente com a BNCC:
Utilizar softwares e aplicativos para explorar transformações geométricas.
Criar projetos interdisciplinares com artes visuais, física e tecnologia.
Trabalhar com problemas contextualizados, como mapas, plantas e design gráfico.
Promover atividades investigativas, como construção de fluxogramas para resolução de problemas.
Autoria de:
Marinez Bronzatti e
Regina Ehlers Bathel.

